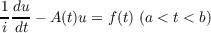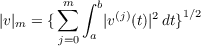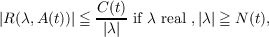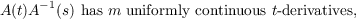|
Consider the differential
equation
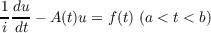 | (1.1) |
where u(t), f(t) are elements of a Hilbert space E and A(t) is a closed linear operator
in E with a domain D(A) independent of t and dense in E. Denote by Cm(a,b) the
set of functions v(t) with values in E which have m strongly continuous derivatives in
(a,b). Introducing the norm
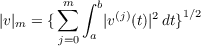 | (1.2) |
where |v(t)| is the E-norm of v(t), we denote by Hm(a,b) the completion with
respect to the norm (1.2) of the subset of functions in Cm(a,b) whose norm is finite.
Set Hm = Hm(−∞,∞) and denote by H0m the subset of functions in Hm which
have compact support. The solutions u(t) of (1.1) are understood in the sense that
u(t) ∈ H1(a′,b′) for any a < a′ < b′ < b.
Theorem 1. Assume that, for each a < t < b, the resolvent R(λ,A(t)) = (λ−A(t))−1
of A(t) exists for all real λ, |λ|≧ N(t), and that
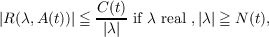 | (1.3) |
where N(t), C(t) are constants. Assume next that for each s ∈ (a,b), A−1(s) exists
and
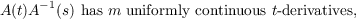 | (1.4) |
for a < t < b, where m is any integer ≧ 1. If u is a solution of (1.1) and if
f ∈ Hm(a,b), then u ∈ Hm+1(a′,b′) for any a < a′ < b′ < b.
Theorem 2. If the assumptions of Theorem 1 hold with m = ∞, if A(t)A−1(s) is
analytic in t(a < t < b) for each s ∈ (a,b), and if f(t) is analytic in (a,b), then u(t) is
also analytic in (a,b).
|