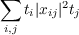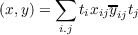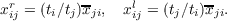On two-sided H^∗-algebras

P. P. Saworotnow

Vol. 16 (1966), No. 2, 365–370

DOI: 10.2140/pjm.1966.16.365

Abstract

We call a Banach algebra A, whose norm is a Hilbert space norm, a two-sided H^∗-algebra if for each x ∈ A there are elements x^l, x^r in A such that (xy,z) = (y,x^lz) and (yx,z) = (y,zx^r) for all y,z ∈ A. A two-sided H^∗-algebra is called discrete is each right ideal R such that {x^r∣x ∈ R} = {x^l∣x ∈ R} contains an idempotent e such that e^r = e^l = e. The purpose of this paper is to obtain a structural characterization of those two-sided H^∗-algebras M which consist of complex matrices x = (x_ij∣i,j ∈ J) (J is any index set) for which

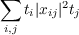
converges. Here t_i is real and 1 ≦ t_i ≦ a for all i ∈ J and some real a. The inner product in M is

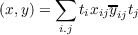
and

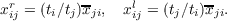
Then every algebra M is discrete simple and proper (Mx = 0 implies x = 0). Conversely every discrete simple and proper two-sided H^∗-algebra is isomorphic to some algebra M. An incidental result is that the radical of a two-sided H^∗-algebra is the right (left) annihilator of the algebra.

Mathematical Subject Classification

Primary: 46.60

Milestones

Received: 2 July 1964

Published: 1 February 1966