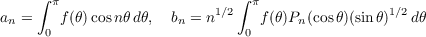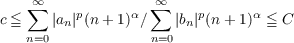|
Let f(𝜃) be integrable on (0,π)
and define
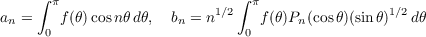
where Pn(x) is the Legendre polynomial of degree n. Then
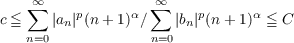 | (1) |
for 1 < p < ∞, −1 < α < p − 1, where C and c depend on p and α but not on f.
From this we obtain a form of the Marcinkiewicz multiplier theorem for Legendre
coefficients. Also an analogue of the Hardy-Littlewood theorem on Fourier coefficients
of monotone coefficients is obtained. In fact, any norm theorem for Fourier
functions can be transplanted by (1) to a corresponding theorem for Legendre
coefficients.
Actually, the main theorem of this paper deals with ultraspherical
coefficients and (1) is just a typical special case, which is stated as above for
simplicity.
|