Permanent of the direct product of matrices

Richard Anthony Brualdi

Vol. 16 (1966), No. 3, 471–482

DOI: 10.2140/pjm.1966.16.471

Abstract

Let A and B be nonnegative matrices of orders m and n respectively. In this paper we derive some properties of the permanent of the direct product A × B of A with B. Specifically we prove that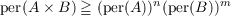

with equality if and only if A or B has at most one nonzero term in its permanent expansion. We also show that every term in the permanent expansion of A × B is expressible as the product of n terms in the permanent expansion of A and m terms in the permanent expansion of B, and conversely. This implies that a minimal positive number K_m,n exists such that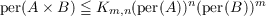

for all nonnegative matrices A and B of orders m and n respectively. A conjecture is given for the value of K_m,n.

Mathematical Subject Classification

Primary: 15.20

Milestones

Received: 23 October 1964

Published: 1 March 1966