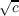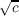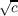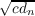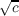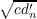|
This paper deals with a special
case of the following problem: Let A, B be matrices of order n over the rational
integers. Compare the algebraic number field generated by the characteristic roots of
AB with those generated by A, B.
We let M(r,s) denote the companion matrix of x2 + rx + s, for rational integers r
and s, and let N(r,s) = M(r,s)(M(r,s))′. Further let F(M(r,s)) and F(N(r,s))
denote the fields generated by the characteristic roots of M(r,s) and N(r,s) over
the rational field, R. This paper is concerned with F(N(r,s)), especially
in relation to F(M(r,s)). The principal results obtained are outlined as
follows:
Let S be the set of square-free integers which are sums of two squares. Then
F(N(r,s)) is of the form R(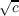 ) where c ∈ S. Further, F(N(r,s)) = R if and only if
rs = 0. Suppose c ∈ S. Then there exist infinitely many distinct pairs of integers
(r,s) such that F(N(r,s)) = R( ) where c ∈ S. Further, F(N(r,s)) = R if and only if
rs = 0. Suppose c ∈ S. Then there exist infinitely many distinct pairs of integers
(r,s) such that F(N(r,s)) = R(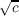 ). ).
Further, if c ∈ S, there exists an infinite sequence {(rn,sn)} of distinct pairs of
integers such that F(M(rn,sn)) = R(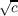 ) and F(N(r
n,sn)) = R( ) and F(N(r
n,sn)) = R(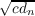 ) for
some integers dn such that (c,dn) = 1. If c ∈ S and c is odd or c = 2, there
exists an infinite sequence {(rn′,sn′)} of distinct pairs of integers such that
F(N(rn′,sn′)) = R( ) for
some integers dn such that (c,dn) = 1. If c ∈ S and c is odd or c = 2, there
exists an infinite sequence {(rn′,sn′)} of distinct pairs of integers such that
F(N(rn′,sn′)) = R(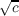 ) and F(M(r
n′,sn′)) = R( ) and F(M(r
n′,sn′)) = R(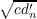 ) for some integers dn′ such
that (c,dn′) = 1. ) for some integers dn′ such
that (c,dn′) = 1.
There are five known pairs of integers (r,s) with rs≠0 and s≠ − 1 such that
F(M(r,s)) and F(N(r,s)) coincide. For s ≡ 2 (mod 4) and for certain odd
integers s the fields F(M(r,s)) and F(N(r,s)) cannot coincide for any integers
r.
Finally, for any integer r≠0 (or s≠0,−1) there exist at most a finite number of
integers s (or r) such that the two fields coincide.
|