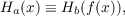|
Spector proved in his
Ph. D. Thesis that if |a| = |b|(a,b ∈ O), then Ha(x) and Hb(x) have the same degree
of unsolvability; Davis had already shown that if |a| = |b| < ω2, then Ha(x) and
Hb(x) are in fact recursively isomorphic, i.e.,
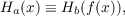 | (1) |
where f(x) is a recursive permutation.
In this note we prove that if |a| = |b| = ξ, then Ha(x) and Hb(x) need not have
the same many-one degree, unless ξ = 0 or is of the form η + 1 or η + ω; if ξ≠0 is not
of the form η + 1 or η + ω, then the partial ordering of the many-one degrees of the
predicates Ha(x) with |a| = ξ contains well-ordered chains of length ω1 as well as
incomparable elements. The proof rests on a combinatorial result which relates the
many-one degree of Ha′(x)(a′ = 3.5a ∈ O) to the rate with which the sequence of
ordinals |an| approaches |a′|.
|