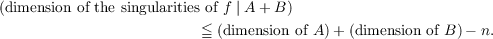|
In this paper we will say that a
piecewise linear map f : K → M from a finite complex into an n-manifold is a
general position (gp) map, if for every pair of simplexes, A, B, contained in K,
By letting B = ∅, we see that a gp map into an n-manifold is an embedding on
each simplex of dimension less than or equal to n. Also note that the restriction of a
gp map to a subcomplex is again a gp map. It is well known that every map f of a
complex into a combinatorial manifold can be homotopically approximated by a gp
map, g, on some subdivision of the complex. One might suppose that, if L is a
subcomplex on which f is already a gp map, then g∣L could be made equat to f∣L.
However, this cannot be done, in general, even if the manifold is a Euclidean space
and the complex is a subdivision of a cell. (See the Remark at the end of
§3.)
In §3 are two general position theorems which fix the map on a subcomplex on
which it is already a gp map, but not without some severe restrictions. These
theorems are stated in terms of relative general position (rgp) which applied to maps
from a pair into a pair. Section 4 considers maps f : (D,BdD) → (M,N) of a
2-manifold, D, into a 3-manifold, M, with 2-submanifold, N, with the added
restriction that f(BdD) ⋅ f(D − BdD) = ∅. It is, in general, impossible in this
setting to make f into an rgp map while keeping f∣BdD fixed. However, two
“relative normal position theorems” are proved which make the singularities “nice”
while not considering a particular subdivision.
|