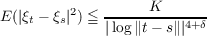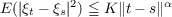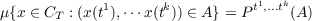|
In this note, Gaussian processes
{ξt;t ∈ H} where H is the Hilbert space l2 are considered. It is shown that if T is a compact
subset of a set of the form {(t1,t2,⋯,tn,⋯) : an ≦ tn ≦ an + 1∕2n,(a1,a2,⋯an,⋯) ∈ H}
(thus including all compact subsets of N-dimensional Eulidean space), and there
exists constants δ > 0 and K > 0 such that
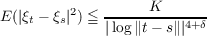
for t,s in H, then almost all sample functions of the process are continuous on T.
Furthermore, if there are constants α > 0 and K such that
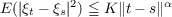
for all t,s in H, then “almost all” sample functions of the process are Lipschitz-β
continuous on T for 0 < β < α∕2. The phrase “almost all” is used in the
sense that the process defines a probability measure μ on the space CT of
continuous or Lipschitz-β continuous functions on T, such that for any k
points t1,t2,⋯tk in T and any Borel set A in k-dimensional Euclidean space
Rk
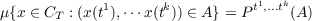
where Pt1,…tk
is the probability measure defined by the random vector {ξt1,⋯ξtk}. In
the case where the process {ξt : t ∈ H} is separable and is separated by the set of
dyadic numbers in H, then the phrase “almost all” as defined here takes on the usual
meaning.
In application, it is shown that the Brownian process in a Hilbert space defined
by Paul Levy satisfies the latter condition for α = 1. Thus almost all sample
functions are Lipschitz-β continuous on T for 0 < β < 1∕2 if T is a compact set
of the form described above. Furthermore, it is shown that Levy’s result
that almost all sample functions of this process are discontinuous in the
Hilbert sphere may be extended to arbitrary noncompact subsets of the form
T = {(t1,t2,⋯,tn,⋯) : an ≦ tn ≦ bn}.
|