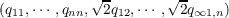|
A real quadratic form
Q = Q(x1,⋯,xn) is called copositive if Q(xI,⋯,xn) ≧ 0 whenever x1,⋯,xn ≧ 0. If we
associate each quadratic form Q = ∑
qijxixjqij = qji(i,j = 1,⋯,n) with a
point
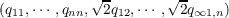
of Euclidean n(n + 1)∕2 space, then the copositive forms constitute a closed convex
cone in this space. We are concerned with the extreme points of this cone. That is,
with those copositive quadratic forms Q for which Q = Q1 + Q2 (with Q1,Q2
copositive) implies Q1 = αQ,Q2 = (1 − a)Q,0 ≦ a ≦ 1. In this paper we limit
ourselves almost entirely to 5-variable forms and announce the discovery of an
hitherto unknown class of extreme copositive quadratic forms in 5 variables. In view
of the known extension process whereby extreme copositive quadratic forms in n
variables may be used to generate extreme forms in n′ variables for any n′ > n > 2,
this new class of forms thus provides new extreme copositive forms in any number of
variables n′≧ 5.
Copositive quadratic forms arise in the theory of inequalities and also in the study
of block designs. The paper of Diananda [2] provides the connection with inequalities
while the paper of Hall and Newman [3] outlines the application of copositive
quadratic forms to block designs.
|