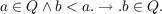|
Spector first constructed a
function h whose degree of recursive unsolvability is minimal—that is to say that any
function recursive in h is either recursive or of the same degree as h. Define a set Q of
degrees to be an initial segment of the upper semi-lattice of degrees of unsolvability
if
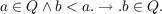
Spector’s result can then be interpreted as saying that a certain partially ordered set
occurs as an initial segment of the degrees; it was conjectured that the same is true
for every finite partially ordered set which has a least member. Sacks then
constructed two minimal degrees a and b such that a ∪ b has a,b,0 as its only
predecessors.
In this paper their methods are extended to obtain the following result. Let T be
the upper semi-lattice of all finite subsets of N. Then T can be embedded as an
initial segment of the degrees. From this it follows that any finite partial
ordering which can be embedded as an initial segment of P(B) (the power
set of B), with B finite, can also be embedded as an initial segment of the
degrees.
|