|
In this paper we shall consider
the reflection of solutions of systems of equations
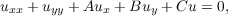 | (1) |
where u = (u1,u2,⋯,un)T,A,B,C are constant, pairwise commutative n × n
matrices, across an analytic arc κ on which the solutions satisfy n analytic linear
differential boundary conditions. If the boundary conditions have coefficients which
are analyiic in a specific preassigned geometrical region cantaining κ, then we shall
show that the solution of (1.1) satisfying such boundary conditions can be extended
across κ, provided certain inequalities are satisfied. Moreover, the region
into which u can be extended will depend only on the analytic arc κ, the
original region, and the coefficients of the boundary conditions; i.e., we shall
have reflection “in the large” and the region will not be restricted by the
equation.
|