Solvability of various boundary value problems for the equation x′′ = f(t,x,x′,x′′) − y

Walter Volodymyr Petryshyn

Vol. 122 (1986), No. 1, 169–195

DOI: 10.2140/pjm.1986.122.169

Abstract

In this paper some of the solvability results of Granas, Guenther and Lee for various homogeneous boundary value problems for the equation x′′ = f(t,x,x′) are extended in an essentially constructive way to the equation (∗) : x′′ = f(t,x,x′,x′′) where f is assumed to satisfy the growth condition: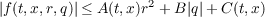

for r, q in R with A and C bounded functions on each compact subset of [0,T] ×R and B in (0,1) and some further conditions stated below. Our proofs are based on the author’s continuation theorem for semilinear A-proper maps and the approach used by Granas, Guenther and Lee in obtaining the a priori bounds for the solutions of equation (∗).

Mathematical Subject Classification 2000

Primary: 34B15

Secondary: 34A45, 34C25

Milestones

Received: 20 August 1984

Revised: 25 February 1985

Published: 1 March 1986