|
|||||

|

|
|

|

|
|
Multipeak solutions
for a singularly perturbed Neumann problem
E.N. Dancer and Shusen Yan |
|
Vol. 189 (1999), No. 2, 241–262
|
Milestones
Received: 12 November 1997
Revised: 29 May 1998
Published: 1 June 1999
|
Authors |
| E.N. Dancer | |
| Shusen Yan | |
| School of Mathematics and
Statistics University of Sydney NSW 2006 Australia |
|
 |
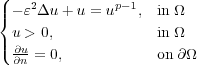
 if
if 