|
|||||

|

|
|

|

|
|
Generic properties of
Whitehead’s algorithm and isomorphism rigidity of random
one-relator groups
Ilya Kapovich, Paul Schupp and Vladimir Shpilrain |
|
Vol. 223 (2006), No. 1, 113–140
|
Abstract |
|
We prove that Whitehead’s algorithm for solving the automorphism problem in a fixed free group Fk has strongly linear time generic-case complexity. This is done by showing that the “hard” part of the algorithm terminates in linear time on an exponentially generic set of input pairs. We then apply these results to one-relator groups. We obtain a Mostow-type isomorphism rigidity result for random one-relator groups: If two such groups are isomorphic then their Cayley graphs on the given generating sets are isometric. Although no nontrivial examples were previously known, we prove that one-relator groups are generically complete groups, that is, they have trivial center and trivial outer automorphism group. We also prove that the stabilizers of generic elements of Fk in Aut(Fk) are cyclic groups generated by inner automorphisms and that Aut(Fk)-orbits are uniformly small in the sense of their growth entropy. We further prove that the number Ik(n) of isomorphism types of k-generator one-relator groups with defining relators of length n satisfies 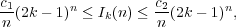 where c1,c2 are positive constants depending on k but not on n. Thus Ik(n) grows in essentially the same manner as the number of cyclic words of length n. |
Keywords
one-relator groups, Whitehead algorithm, generic-case
complexity
|
Mathematical Subject Classification 2000
Primary: 20P05
Secondary: 03D15, 20F36, 57M05, 68W40
|
Milestones
Received: 24 April 2004
Revised: 11 August 2004
Accepted: 24 August 2004
Published: 1 January 2006
|
Authors |
| Ilya Kapovich | |
| Department of Mathematics University of Illinois at Urbana–Champaign 1409 West Green Street Urbana, IL 61801 |
|
| http://www.math.uiuc.edu/~kapovich/ | |
| Paul Schupp | |
| Department of Mathematics University of Illinois at Urbana–Champaign 1409 West Green Street Urbana, IL 61801 |
|
| http://www.math.uiuc.edu/People/schupp.html | |
| Vladimir Shpilrain | |
| Department of Mathematics The City College of New York New York, NY 10031 |
|
| http://www.sci.ccny.cuny.edu/~shpil | |
 |
