|
|||||

|

|
|

|

|
|
Fourier transforms of
semisimple orbital integrals on the Lie algebra of
SL2
Loren Spice |
|
Vol. 254 (2011), No. 2, 407–448
|
Abstract |
|
The Harish-Chandra–Howe
local character expansion expresses the characters of reductive, |
Keywords
p-adic, orbital integral,
special function
|
Mathematical Subject Classification 2010
Primary: 22E35, 22E50
|
Milestones
Received: 7 October 2010
Accepted: 11 April 2011
Published: 27 February 2012
|
Authors |
| Loren Spice | |
| Department of Mathematics Texas Christian University TCU Box 298900 2840 W. Bowie St Fort Worth, TX 76109 United States |
|
| http://faculty.tcu.edu/lspice | |
 |
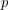 -adic groups in
terms of Fourier transforms of nilpotent orbital integrals on their Lie algebras, and
Murnaghan–Kirillov theory expresses many characters of reductive,
-adic groups in
terms of Fourier transforms of nilpotent orbital integrals on their Lie algebras, and
Murnaghan–Kirillov theory expresses many characters of reductive, 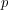 -adic groups
in terms of Fourier transforms of semisimple orbital integrals (also on their Lie
algebras). In many cases, the evaluation of these Fourier transforms seems
intractable, but for
-adic groups
in terms of Fourier transforms of semisimple orbital integrals (also on their Lie
algebras). In many cases, the evaluation of these Fourier transforms seems
intractable, but for 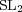 , the nilpotent orbital integrals have already been
computed. We compute Fourier transforms of semisimple orbital integrals using a
variant of Huntsinger’s integral formula and the theory of
, the nilpotent orbital integrals have already been
computed. We compute Fourier transforms of semisimple orbital integrals using a
variant of Huntsinger’s integral formula and the theory of 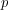 -adic special
functions.
-adic special
functions.