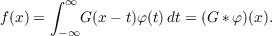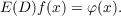|
The convolution transform is
defined by the equation
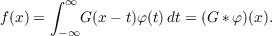 | (1.1) |
If the kernel G(t) has a bilateral Laplace transform which is the reciprocal of an
entire function E(s), then E(s) is called the inversion function of the transform. This
terminology is appropriate in view of the fact that the transform (1.1) is inverted, in
some sense, by the operator E(D), where D stands for differentiation with respect to
x:
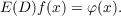 | (1.2) |
It is the purpose of the present paper to prove (1.2) when the roots of E(s) are
allowed to be genuinely remote from the real axis.
|