|
For a fixed positive integer n,
let Q be the set of all n-dimensional lattice points (x1,⋯,xn) with each xi a
nonnegative integer and at least one xi positive. A finite nonempty subset
R of Q is called a fundamental set if for every (r1,⋯,rn) in R, all vectors
(x1,⋯,xn) of Q with xi ≦ ri, i = 1,⋯,n, are also in R. If A is any subset of Q
and R is any fundamental set, let A(R) denote the number of vectors in
A ∩ R. Finally, if A is any proper subset of Q, let the density of A be the
quantity
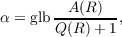
taken over all fundamental sets R for which A(R) < Q(R). Then the theorem proved
in this paper can be stated as follows.
Theorem. Let A and B be subsets of Q, let C be the set of all vectors of the form
a, b, or a + b where a ∈ A and b ∈ B, let α be the density of A, and let R be any
fundamental set such that (1) there exists at least one vector in R which is not in C,
and (2) for each b in B ∩R (if any) there exists g in R but not in C such that g −b is
in Q. Then
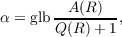
![C (R) ≧ α ⌈Q (R)+ 1]+ B(R ).](a151x.png)
|
