On simple extended Lie algebras over fields of characteristic zero

Arthur Argyle Sagle

Vol. 15 (1965), No. 2, 621–648

DOI: 10.2140/pjm.1965.15.621

Abstract

In this paper we shall investigate algebras which generalize Lie algebras, Malcev algebras and binary-Lie algebras (every two elements generate a Lie subalgebra). Such an algebra A is called an extented Lie algebra (briefly el-algebra) and is defined by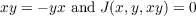

for all x, y in A where J(x,y,z) = xy ⋅ z + yz ⋅ x + zx ⋅ y. We prove the following.

Theorem. Let A be a simple finite dimensional el-algebra over an algebraically closed field of characteristic zero, then A is a simple Lie algebra or the simple seven dimensional Malcev algebra if and only if the trace form, (x,y) = trace R_xR_y, is a nondegenerate invariant form.

Mathematical Subject Classification

Primary: 17.30

Milestones

Received: 7 November 1963

Published: 1 June 1965