Proper ordered inverse semigroups

Tôru Saitô

Vol. 15 (1965), No. 2, 649–666

DOI: 10.2140/pjm.1965.15.649

Abstract

Let S be an ordered inverse semigroup, that is, an inverse semigroup with a simple order < which satisfies the condition: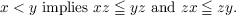

Let E be the subsemigroup of S constituted by all the idempotents of S. By a result of Munn, Γ = S∕σ is an ordered group, where σ is the congruence relation such that xσy if and only if ex = ey for some e ∈ E. An ordered inverse semigroup S is called proper if the σ-class I which is the identity element of Γ contains only idempotents of S.

In a proper ordered inverse semigroup S, let Γ(e)(e ∈ E) be the set of those members of Γ which intersect nontrivially with R_e. Each element of S can be represented in the form (α,e), where e ∈ E and α ∈ Γ(e). We define e^α = a⁻¹a ∈ E, where a = (α,e). Then Γ(e) and e^α satisfy the following six conditions:

(i) ⋃ _e∈EΓ(e) = Γ;

(ii) I ∈ Γ(e) and e^I = e;

(iii) if f ≦ e in the semilattice with respect to the natural ordering of the commutative idempotent semigroup E and α ∈ Γ(e), then α ∈ Γ(f) and f^α ≦ e^α in the semilattice E;

(iv) if α ∈ Γ(e) and β ∈ Γ(e^α), then αβ ∈ Γ(e) and e^αβ = (e^α)^β;

(v) if α ∈ Γ(e), then α⁻¹ ∈ Γ(e^α);

(vi) if α ∈ Γ(e) ∩ Γ(f) and e ≦ f, then e^α ≦ f^α.

Also the product and the order in S determined by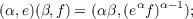

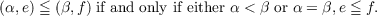
Next we prove conversely a theorem asserting that, for an ordered commutative idempotent semigroup E and an ordered group Γ, if Γ(e) and e^α satisfy the six conditions above, then the set {(α,e);e ∈ E,α ∈ Γ(e)} is a proper ordered inverse semigroup with respect to the product and the order mentioned above. Besides this, we present other characterizations of special cases.

Mathematical Subject Classification

Primary: 06.70

Secondary: 20.00

Milestones

Received: 14 April 1964

Published: 1 June 1965