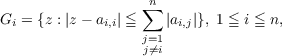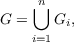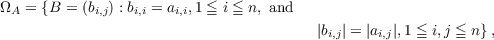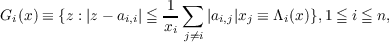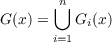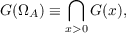Minimal Gerschgorin sets

Richard Steven Varga

Vol. 15 (1965), No. 2, 719–729

DOI: 10.2140/pjm.1965.15.719

Abstract

If A = (a_i,j) is a fixed n × n complex matrix, then it is well known that the Gerschgorin disks G_i in the complex plane, defined by

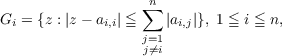(1)

are such that each eigenvalue of A lies in at least one disk, and, consequently, the union of these disks,

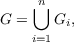(2)

which we call the Gerschgorin set, contains all the eigenvalues of A. It is however clear from (1) that the radii of these Gerschgorin disks depend only on the moduli of the off-diagonal entries of A. Thus, if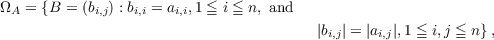

(3)

then it is clear that the Gerschgorin set G contains all the eigenvalues of each n×n matrix B in Ω_A. It is natural to ask how far-reaching this elementary theory is in bounding the eigenvalues of Ω_A.

To extend the above results slightly, let x > 0 be any vector with positive components, and let X(x) ≡ diag(x₁,x₂,⋯,x_n). Applying the above results to X⁻¹(x)AX(x) shows that if

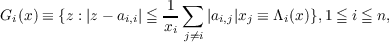(1’)

then the associated Gerschgorin set

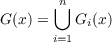(2’)

again contains all the eigenvalues of each B ∈ Ω_A for every x > 0. Thus, the closed bounded set

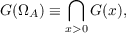(4)

which we call the minimal Gerschgorin set, also contains all the eigenvalues of each B ∈ Ω_A.

One of the major results in this paper is that each boundary point of G(Ω_A) is an eigenvalue of some matrix B in Ω_A.

Mathematical Subject Classification

Primary: 15.25

Milestones

Received: 12 September 1963

Revised: 20 December 1963

Published: 1 June 1965