A note on multiple exponential sums

L. Carlitz

Vol. 15 (1965), No. 3, 757–765

DOI: 10.2140/pjm.1965.15.757

Abstract

Put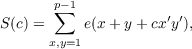

Where e(x) = e^2πi∕p and xx′≡ yy′≡ 1 (mod p), Mordell has conjectured that S(c) = O(p). The writer shows first, by an elementary argument that S(c) = O(p^3∕2). Next he proves, using a theorem of Lang and Weil that S(c) = O(p^11∕8). Finally he proves that S(c) = O(p^5∕4); the proof makes use of the estimate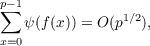

where ψ(a) is the Legendre symbol and f(x) is a polynomial of the fourth degree.

Mathematical Subject Classification

Primary: 10.41

Milestones

Received: 28 July 1964

Revised: 23 September 1964

Published: 1 September 1965