|
|||||

|

|
|

|

|
|
Symmetric dual
nonlinear programs
George Bernard Dantzig, E. Eisenberg and Richard Warren Cottle |
|
Vol. 15 (1965), No. 3, 809–812
|
Abstract |
|
Consider a function K(x,y) continuously differentiable in x ∈ Rn and y ∈ Rm. We form two problems: PRIMAL: Find (x,y) ≧ 0 and Min F such that 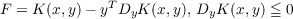
DUAL: Find (x,y) ≧ 0 and Max G such that 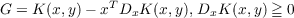 where DyK(x,y) and DxK(x,y) denote the vectors of partial derivatives DyiK(x,y) and DxjK(x,y) for i = 1,⋯,m and j = 1,⋯,n. Our main result is the existence of a common extremal solution (x0,y0) to both the primal and dual systems when (i) an extremal solution (x0,y0) to the primal exists, (ii) K is convex in x for each y, concave in y for each x and (iii) K, twice differentiable, has the property at (x0,y0) that its matrix of second partials with respect to y is negative definite. |
Mathematical Subject Classification
Primary: 90.58
|
Milestones
Received: 23 January 1964
Published: 1 September 1965
|
Authors |
| George Bernard Dantzig | |
| E. Eisenberg | |
| Richard Warren Cottle | |
 |
