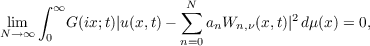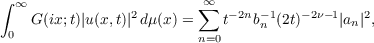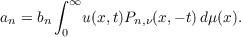|
The object of this paper is
to characterize functions which have L2 expansions in terms of polynomial solutions
Pn,ν(x,t) of the generalized heat equation
![∂2-- 2ν-∂-- ∂-
[∂x2 + x ∂x]u(x,t) = ∂tu(x,t).](a130x.png) | (*) |
and in terms of the Appell transforms Wn,ν(x,t) of the Pn,ν(x,t). H∗ denotes
the C2 class of functions u(x,t) which, for a < t < b, satisfy (*) and for
which
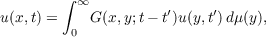
![dμ(x) = 2(1∕2)− ν[Γ (ν + 12)]−1x2ν dx,](a132x.png)
for all t, t′, a < t′ < t < b, the integral converging absolutely, where G(x,y;t) is the
source solution of (*). The principal results are the following:
Theorem. Let u(x,t) ∈ H∗, − σ ≦ t < 0, and
![1 2
u(x,t)[G(x;− t)]2 ∈ L](a133x.png)
for each fixed t − σ ≦ t < 0, 0 ≦ x < ∞. Then, for −σ ≦ t < 0,
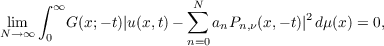
and
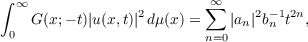
where
![Γ (ν + 1)
bn = [24nn!]−1-----12---,
Γ (ν + 2 + n)](a136x.png)
and
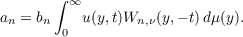
Theorem. If u(x,t) ∈ H∗, 0 < t ≦ σ, and if
![u(ix,t)[G(x;t)]12 ∈ L2](a138x.png)
for each fixed t, 0 < t ≦ σ, 0 ≦ x < ∞, then, for 0 < t ≦ σ,
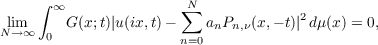
and
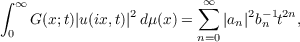
where bn is given above and
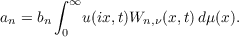
Theorem. If u(x,t) ∈ H∗, 0 < σ ≦ t, and if
![1
u(x,t)[G (ix;t)]2 ∈ L2](a1312x.png)
for each fixed t, 0 < σ ≦ t, 0 ≦ x < ∞, then, for 0 < σ ≦ t,
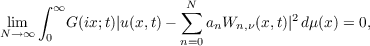
and
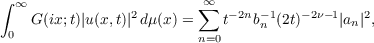
where bn is given above and
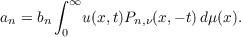
|





![∂2-- 2ν-∂-- ∂-
[∂x2 + x ∂x]u(x,t) = ∂tu(x,t).](a130x.png)
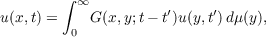
![dμ(x) = 2(1∕2)− ν[Γ (ν + 12)]−1x2ν dx,](a132x.png)
![1 2
u(x,t)[G(x;− t)]2 ∈ L](a133x.png)
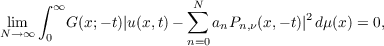
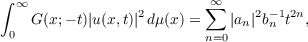
![Γ (ν + 1)
bn = [24nn!]−1-----12---,
Γ (ν + 2 + n)](a136x.png)
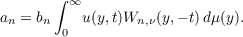
![u(ix,t)[G(x;t)]12 ∈ L2](a138x.png)
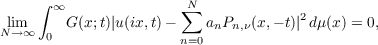
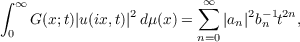
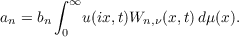
![1
u(x,t)[G (ix;t)]2 ∈ L2](a1312x.png)