A subdeterminant inequality

Marvin David Marcus and H. Minc

Vol. 15 (1965), No. 3, 921–924

DOI: 10.2140/pjm.1965.15.921

Abstract

Let A be an n-square positive semi-definite hermitian matrix and let D_m(A) denote the maximum of all order m principal subdeterminants of A. In this note we prove the inequality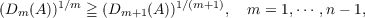

and discuss in detail the case of equality. This result is closely related to Newton’s and Szász’s inequalities.

Mathematical Subject Classification

Primary: 15.58

Secondary: 15.20

Milestones

Received: 27 August 1964

Published: 1 September 1965