|
Let (X,S,μ) be a σ-finite
non-atomic measure space let N be a real valued continuous convex even function
defined on the real line such that
(1) N(u) is nondecreasing for u ≧ 0,
(2) limu→∞N(u)∕u = ∞,
(3) limu→0N(u)∕u = 0.
Let LN be the set of all real valued μ-measurable functions f such that
∫
XN(f)dμ < ∞. It is known that if there exists a constant k such that
N(2u) ≦ kN(u) for all u ≧ 0 then LN is a linear space; in fact, LN is a B-Space if a
norm ∥⋅∥ is defined by setting
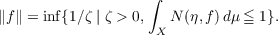 | (*) |
Denoting the B-space (LN,∥⋅∥) by LN∗ it is proposed to obtain the necessary and
sufficient conditions in order that LN∗ may be (1) Strictly Convex (2) Uniformly
Convex.
|