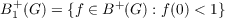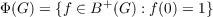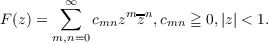Functions which operate on characteristic functions

Alan G. Konheim and Benjamin Weiss

Vol. 15 (1965), No. 4, 1279–1293

DOI: 10.2140/pjm.1965.15.1279

Abstract

Let G be a locally compact abelian group and B⁺(G) the family of continuous, complex-valued non-negative definite functions on G. Set

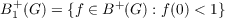
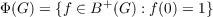
A complex-valued function defined on the open unit disk is said to operate on {B₁⁺(G),B⁺(G)} if f ∈ B₁⁺(G) implies F(f) ∈ B⁺(G), similarly for {Φ(G),Φ(G)}. Recently C. S. Herz has given a proof of a conjecture of W. Rudin that F operates on {B₁⁺(G),B⁺(G)} if and only if

(*)

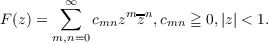for a certain class of G. We shall show by independent methods that F operates on Φ(R¹) if F is given by (*) for |z|≦ 1 and F(1) = 1. This answers a question posed by E. Lukacs and provides in addition an alternate proof of Herz’s theorem.

Mathematical Subject Classification

Primary: 42.54

Secondary: 60.08

Milestones

Received: 20 June 1964

Revised: 23 August 1964

Published: 1 December 1965