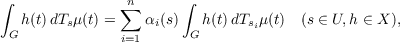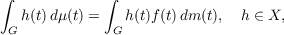|
Let μ be a regular complex-valued
Borel measure on a locally compact topological (LC) group G which is finite on
compact sets; and for each s ∈ G define the measure Tsμ by Tsμ(E) = μ(E + s),
E ∈ Bc(G) the collection of all Borel subsets of G with compact closure. If f is a
function on G then for each s ∈ G we set Tsf(t) = f(t + s), t ∈ G. Let X be a
translation invariant subspace of C0(G), the space of continuous complex-valued
functions on G which vanish at infinity, i.e., a subspace such that f ∈ X implies
T−sf ∈ X, s ∈ G; and let U be an open symmetric neighborhood of zero in G. Then
we shall say μ acts U-almost invariantly on X if ∫
G|h(t)|d|μ|(t) < ∞, h ∈ X,
and
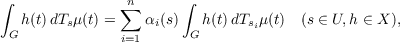
where s1,s2,⋯,sn are fixed elements of U. We shall say μ is a U-almost invariant
measure on G if {Tsμ∣s ∈ U} spans a finite dimensional space of measures. When
U = G we shall say μ acts almost invariantly and μ is an almost invariant
measure, respectively. The main results of this paper show that if μ acts
U-almost invariantly on X then there exists some continuous function f such
that
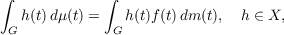
where dm is right invariant Haar measure on G; and that μ is a U-almost invariant
measure if and only if there exists a continuous f such that dμ(t) = f(t)dm(t) and
{Tsf∣s ∈ U} spans a finite dimensional space of functions.
|