Some results in the location of zeros of polynomials

Zalman Rubinstein

Vol. 15 (1965), No. 4, 1391–1395

DOI: 10.2140/pjm.1965.15.1391

Abstract

Three out of the four theorems proved in this paper deal with the location of the zeros of a polynomial P(z) whose zeros z_i, i = 1,2,⋯,n satisfy the conditions |z_i|≦ 1, and ∑ _i=1ⁿz_i^p = 0 for p = 1,2,⋯,l. One of those estimates is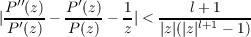

for |z| > 1.

The fourth result is of a different nature. It refines, in particular, a theorem due to Eneström and Kakeya. It is shown that no zero of the polynomial h(z) = ∑ _k=0ⁿb_kz^k lies in the disk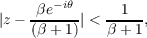

where β = max_|z|=1|h′(z)|∕max_|z|=1|h(z)|, and max_|z|=1|h(z)| = |h(e^i𝜃)|.

Mathematical Subject Classification

Primary: 30.11

Milestones

Received: 3 June 1964

Published: 1 December 1965