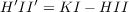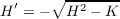|
Two imbedding fundamental
forms determine (up to motions) the smooth imbedding of an oriented surface
in E3. The situation is, however, substantially different for the sufficiently
smooth conformal imbedding of a Riemann surface R in E3. Conventionally
such an imbedding is achieved by a conformal correspondence between R
and the Riemann surface R1 determined on a smoothly imbedded oriented
surface S in E3 by its first fundamental from I. We show that except where
H ⋅ K = 0 on S, such an R1 conformal imbedding of R in E3 is determined
(up to motions) by the second fundamental form II on S, expressed as a
form on R. In particular, I is determined by II on R1, where H ⋅ K≠0 on
S.
Similar remarks are valid for two less standard methods of conformal imbedding.
If an oriented surface S is smoothly imbedded in E3 so that H > 0 and K > 0, then
II defines a Riemann surface R2 on S. And, if S is imbedded so that K < 0, then II′
given by
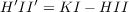
with
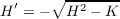
defines a Riemann surface R2′ on S. Thus a conformal correspondence between R
and R2 (or R2′) is called an R2 (or R2′) conformal imbedding of R in E3. We show
that I on S, expressed as a form on R, determines the R2 or (wherever H≠0 and sign
H is know) the R2′ imbedding of R in E3 (up to motions). In particular, I
determines II on R2, and (where H≠0, and sign H is known) on R2′ as
well. Finally, we give restatements of the fundamental theorem of surface
theory in forms appropriate to R1, R2 and R2′ conformal imbeddings in
E3.
|