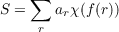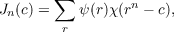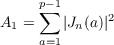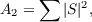Some averages of character sums

Herbert Walum

Vol. 16 (1966), No. 1, 189–192

DOI: 10.2140/pjm.1966.16.189

Abstract

Let χ and ψ be nonprincipal characters mod p. Let f be a polynomial mod p and let a₁,⋯,a_p be complex constants. We will assume a_j = a_k for j ≡ k(p), and thus have a_n defined for all n. Define

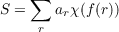(1)

and

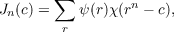(2)

where the variables of summation run through a complete system of residues mod p.

The averages in question are

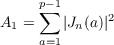(3)

and

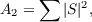(4)

where the sum in (4) is over the coefficients mod p of certain fixed powers of the variables in f. Exact formulae for A₁ will be obtained in all cases, and for A₂ in an extensive class of cases.

Specifically, the following theorems are true.

Mathematical Subject Classification

Primary: 10.41

Milestones

Received: 21 November 1963

Revised: 16 June 1964

Published: 1 January 1966