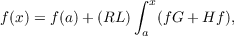|
H. S. Wall, J. S. MacNerney
and T. H. Hildebrandt have shown interdependencies between the equations
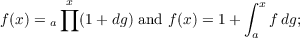
this paper extends and consolidates some of their results. Let S be a linearly ordered
set, R be a normed ring, and OA0 and OM0 be classes of functions G from S ×S to
R for which
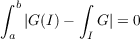
and
![∫ b ∏
|[1+ G (I)]− (1 + G)| = 0,
a I](a102x.png)
respectively. We show the following. If G has bounded variation, G ∈ OA0 if and
only if G ∈ OM0. For some rings, the existence of ∫
abG(I) and a ∏
b[1 + G(I)] imply
that G ∈ OA0 and OM0, respectively. This is used to prove a product integral
solution of integral equations such as
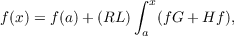
where f is a function from S to R and G and H are functions from S × S to R.
Then these results are used (a) to show that each nonsingular m × m matrix of
complex numbers has n distinct n-th roots, (b) to show that, with some restrictions,
∑
i=1∞Ai exists if and only if ∏
i=1∞(1 + Ai) exists and (c) to find solutions of
integrals equations such as

|




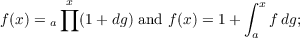
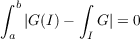
![∫ b ∏
|[1+ G (I)]− (1 + G)| = 0,
a I](a102x.png)