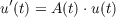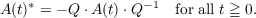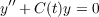|
In this paper we study the
stability of the solutions of the differential equation
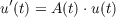 | (1) |
for t ≧ 0 in a separable Hilbert space. It is assumed that A(t) is periodic with period
one and satisfies the following symmetry condition: There exists a continuous
constant invertible operator Q such that
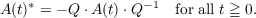
We use a perturbation technique. Let A(t) = A0(t) + B(t) where A0(t) is compact
and antihermitian for all t. We denote by U0(t) the solution operator of
u′(t) = A0(t)u(t). It is shown that (1) is stable if B(t) satisfies a certain smallness
condition involving the distribution of the eigenvalues of U0(1) and the action of B(t)
on the eigenvectors of U0(1). The results can be applied to the second order
equation
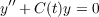
where C(t) is selfadjoint for all t.
|