|
This paper deals with regressive
functions and regressive isols. It was proven by J. C. E. Dekker in [2] that the
collection ΛR of all regressive isols is not closed under addition. In the first
note of this paper we shall given another proof of this fact by considering a
new relation, denoted by 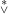 , between infinite regressive isols. Let A and B
denote infinite regressive isols. The main results established in the first note
are: , between infinite regressive isols. Let A and B
denote infinite regressive isols. The main results established in the first note
are:
(1) A ≦∗B⇒A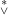 B, yet not conversely. B, yet not conversely.
(2) A + B ∈ ΛR⇒A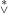 B, yet not conversely. B, yet not conversely.
(3) There exist infinite regressive isols which are not 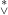 related. related.
(4) ΛR is not closed under addition.
In addition, the following result is stated.
(5) A + B ∈ ΛR⇒min(A,B) ≦ A + B, yet not conversely.
In the second note we consider the ≦∗ relation between regressive isols. A natural
question concerning this relation is whether A ≦∗B, where A and B are
regressive isols, is a necessary or a sufficient condition for the sum A + B to be
regressive. In the second note we show that this condition is neither necessary nor
sufficient.
We shall assume that the reader is familiar with the notations, terminology and
main results of [1] and [2].
|





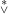 , between infinite regressive isols. Let
, between infinite regressive isols. Let 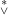
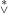
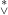 related.
related.
