|
|||||

|

|
|

|

|
|
Two inequalities in
nonnegative symmetric matrices
David London |
|
Vol. 16 (1966), No. 3, 515–536
|
Abstract |
|
Marcus and Newman have made the following conjecture: Let A = (aij) be a n × n nonnegative symmetric matrix. Then 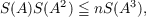 where 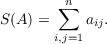 After reducing the conjecture to a standard maximum problem of linear programming we prove that it holds for n ≦ 3. A counter example shows that for n ≧ 4 the conjecture is wrong. We also consider the following conjecture: Let A = (aij) be a n × n nonnegative symmetric matrix. Then 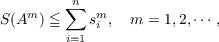 where 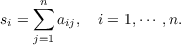 The validity of this conjecture is established in two cases: (1) m up to 5 and any n, (2) n up to 3 and any m. The general case remains open. We conclude this paper with two generalizations of the second theorem. |
Mathematical Subject Classification
Primary: 15.58
|
Milestones
Received: 8 October 1964
Published: 1 March 1966
|
Authors |
| David London | |
 |
