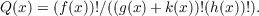|
Let f(x), g(x), and h(x) be
rational integer coefficient polynomials of positive degree and with positive leading
coefficients and satisfying
 | (1.1) |
k(x) also being such a polynomial of degree ≧ 0, let
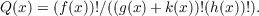 | (1.2) |
Question 1: Is Q(x) integral for an infinity of integers x, at least when k(x) of
degree zero, say k(x) = k(≧ 1)?
Question 2: Is Q(x) nonintegral for all sufficiently large integers x, at least
when the degree of k(x) is ≧ 1? No general answer is known to both these
questions. In this paper, we consider the question of existence of an infinity of
integers x for which Q(x) is not an integer: in the context of question 1, we
obtain certain conditions on the coefficients of g(x) and h(x) and k to ensure
the existence of an infinity of integers x for which Q(x) is not an integer,
and in the context of question 2, we prove Q(x) is nonintegral infinitely
often.
|