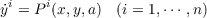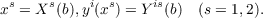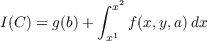|
An arc C is a collection of
parameters bρ (ρ = 1,⋯,r) on an open set B and sets of functions yi(x),
ah(x)(i = 1,⋯,n;h = 1,⋯,m) defined on an interval x1 ≦ x ≦ x2 with yi(x)
continuous and ẏi(x), ah(x) piecewise continuous. The arc is admissible if it satisfies
the differential equations
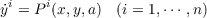
on x1 ≦ x ≦ x2 and the end conditions
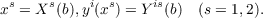
The dot denotes differentiation with respect to x. The problem at hand
is to find in a class of admissible arcs C, an arc C0, which minimizes the
integral
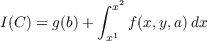
where P(x,y,a) and f(x,y,a) are assumed to be class C′′ for (x,y,a) in an open set
R while g(b), Xs(b), Y is(b) are of class C′′ on B. Under the added assumption that
P(x,y,a) is Lipschitzian in y and a, the indirect method of Hestenes is used to prove
that the necessary conditions for relative minima of the problem above,
strengthened in the usual manner, yield a set of sufficient conditions. This problem
differs from that of Pontryagin in the choice of (x,y,a) to lie in an open
set.
|