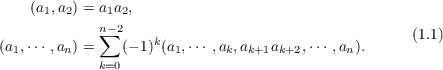|
This paper is concerned
with certain classes of nonassociative rings. These rings are defined by first extending
the associator (a,b,c) = (ab)c − a(bc). The n-associator (a1,⋯,an) is defined
by
A ring is defined to be n-associative if the n-associator vanishes in the ring. It is
shown that simple 4-associative and simple 5-associative rings are associative; simple
2k-associative rings are (2k − 1) associative or have zero center; and simple,
commutative n-associative rings, 6 ≦ n ≦ 9, are associative. The concept of rings
which are associative of degree 2k + 1 is defined, and it is shown that simple,
commutative rings which are associative of degree 2k + 1 are associative.
The characteristic of the ring is slightly restricted in all but one of these
results.
|