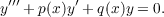|
This paper is a
study of the oscillation and other properties of solutions of the differential
equation
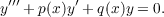 | (L) |
Throughout, we shall assume that p(x) and q(x) are continuous and do
not change sign on the infinite half-axis I : a ≦ x < +∞. A solution of (L)
will be said to be oscillatory if it change sign for arbitrarily large values of
x.
Our principal results will be concerned with the existence, uniqueness, (aside from
constant multiples) and asymptotic behavior of nontrivial, nonoscillatory solutions,
and criteria for the existence of oscillatory solutions in terms of the behavior of
nonoscillatory solutions. Other results are concerned with separation properties and
the question of when the amplitudes of oscillatory solutions are increasing or
decreasing.
|