Cohomology of cyclic groups of prime square order

Judy Parr

Vol. 17 (1966), No. 3, 467–473

DOI: 10.2140/pjm.1966.17.467

Abstract

Let G be a cyclic group of order p², p a prime, and let U be its unique proper subgroup. If A is any G-module, then the four cohomology groups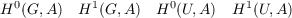

determine all the cohomology groups of A with respect to G and to U. This article determines what values this ordered set of four groups takes on as A runs through all finitely generated G-modules.

Mathematical Subject Classification

Primary: 18.20

Milestones

Received: 27 December 1963

Published: 1 June 1966