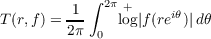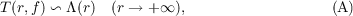|
Let f(z) be analytic in the
region |z| < R (R ≦ +∞). Then in the interval 0 ≦ r < R, Nevanlinna’s
characteristic
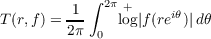
is known to be nonnegative, nondecreasing and convex in log r; however, it is not
known whether these properties characterize completely T(r,f).
Recently, A. Edrei and W. H. J. Fuchs have investigated one aspect of this
question; they have shown that if Λ(r) is an arbitrary convex function of log r defined
for r0 ≦ r < +∞ and such that log r = o(Λ(r)) as r → +∞, then it is possible to find
an entire function f(z) such that
except possibly for values of r belonging to an exceptional set of finite measure. In
this note I establish an analogue of this result for the case of functions regular in a
disk of finite radius R.
|