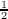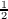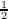Vol. 18, No. 1, 1966
Download this article
Download this article. For screen
For printing
Recent Issues
Vol. 332: 1  2
Vol. 331: 1  2
Vol. 330: 1  2
Vol. 329: 1  2
Vol. 328: 1  2
Vol. 327: 1  2
Vol. 326: 1  2
Vol. 325: 1  2
Online Archive
Volume:
Issue:
     
The Journal
About the journal
Ethics and policies
Peer-review process
 
Submission guidelines
Submission form
Editorial board
Officers
 
Subscriptions
 
ISSN 1945-5844 (electronic)
ISSN 0030-8730 (print)
 
Special Issues
Author index
To appear
 
Other MSP journals
Toeplitz forms and ultraspherical polynomials

Jeffrey Davis and Isidore Isaac Hirschman, Jr.
Vol. 18 (1966), No. 1, 73–95
DOI: 10.2140/pjm.1966.18.73
Abstract

For a fixed ν > 0 we set

2n(ν + 12)nW ν(n,x) = (− 1)n(1− x2)−v+1∕2(ddx)n[(1 − x2)n+ν−1∕2]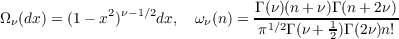

where (ν + 1 2)n = Γ(ν + 1 2 + n)∕Γ(ν + 1 2). The Wν(n,x) are the ultraspherical polynomials of index ν normalized so that Wν(n,1) = 1. If

2 ν−1∕2 Γ (ν-)(n-+ν-)Γ (n-+-2ν) Ων(dx) = (1− x ) dx, ων(n) = π1∕2Γ (ν + 12)Γ (2ν)n!

then the Wν(n,x) satisfy the orthogonality relations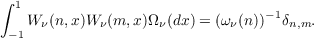

∫ 1W (n,x)W (m, x)Ω (dx) = (ω (n ))−1δ . −1 ν ν ν ν n,m

Because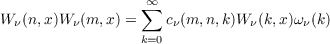

∞ W ν(n,x)W ν(m,x) = ∑ cν(m, n,k)W ν(k,x)ων(k) k=0

where the cν(m,n,k) are nonnegative, the [Wν(n,x)]n=0∞ behave rather like characters on a compact group. Consequently certain portions of harmonic analysis, which do not extend to orthogonal polynomials in general, have interesting analogues for ultraspherical polynomials.

In the present paper this fact is exploited to study the moments of the eigenvalues of generalized Toeplitz matrices constructed using ultraspherical polynomials.
Mathematical Subject Classification
Primary: 33.27
Milestones
Received: 11 March 1965
Published: 1 July 1966
Authors
Jeffrey Davis
Isidore Isaac Hirschman, Jr.