|
If G is a group and T is a
nonempty subset of G, we say that T divides G if and only if G contains a subset S
such that every element of G has a unique representation as ts with t in T, s in S, in
which case we write T ⋅ S = G. We study the case where G is Σn, the symmetric
group on n symbols and T is the set consisting of the identity and all transpositions
in Σn.
The problem may be given a combinatorial setting as follows: For x, y in
Σn, let d(x,y) be the minimum number of transpositions needed to write
xy−1. One verifies that d converts Σn into a metric space, and that T divides
Σn if and only if Σn can be covered by disjoint closed spheres of radius
one.
We use the irreducible characters of Σn, together with judiciously selected
permutation representations of Σn, to prove the following result.
Theorem. If 1 + (n(n − 1))∕2 is divisible by a prime exceeding 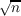 + 2, then T
does not divide Σn.
|
