|
|||||

|

|
|

|

|
|
On the functional
equation F(mn)F((m,
n)) = F(m)F(n)f((m,n))
James E. Shockley |
|
Vol. 18 (1966), No. 1, 185–189
|
Abstract |
|
Let f be a multiplicative arithmetic function, f(1) = 1. Necessary and sufficient conditions on f will be found so that the functional equation 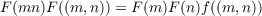 will have a solution F with F(1)≠0 and all solution F will be determined. It will be shown that two different types of solutions may exist and that one of these requires that f have a property similar to complete multiplicativity. |
Mathematical Subject Classification
Primary: 10.43
|
Milestones
Received: 23 October 1964
Revised: 24 February 1965
Published: 1 July 1966
|
Authors |
| James E. Shockley | |
 |
