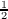|
The kernel of a cooperative
game is a subset of the bargaining set ℳ1(i). It is sensitive to symmetry relations
and their generalizations, which may exist in the characteristic function. The present
paper offers an interesting representation formula for the kernel. This formula is
applied to deriving properties of the kernel as well as practical methods for its
computation.
In particular, we provide an algebraic proof to the theorem stating that for each
coalition structure in a cooperative game there exists a payoff in the kernel (and
therefore also in the bargaining set ℳ1(i)). (All other known proofs of this theorem
are based on the Brouwer fixed-point theorem.) We also prove that the maximal
dimension of the kernel of an n-person game is n− [log 2(n−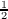 )] − 2, and this bound
is sharp. )] − 2, and this bound
is sharp.
Two players in a game are called symmetric, if the game remains invariant when
these players exchange roles. One generalizes this concept by defining a player k to be
more desirable than a player l, if player k always contributes not less than
player l by joining coalitions which contain none of these players. It turns out
that the payoffs in the kernel always preserve the order determined by the
desirability relations. This fact may simplify the representation formula
significantly.
|