|
|||||

|

|
|

|

|
|
nth order integral operators associated with
Hilbert transforms
G. O. Okikiolu |
|
Vol. 18 (1966), No. 2, 343–360
|
Abstract |
||||||||||||||||
|
In this paper, we study the n-th order analogues of certain integral operators allied to the Hilbert transform and to Dirichlet’s integrals. Most of the results known to be true for n = 0 are proved for the general case. Some cases in which the analogy fails are also considered. Among the integrals considered are transforms Bα(n)(f) and Iα(n)(f) defined by
|
Mathematical Subject Classification
Primary: 44.30
|
Milestones
Received: 15 April 1965
Published: 1 August 1966
|
Authors |
| G. O. Okikiolu | |
 |
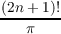 (P.V.)
(P.V.) 
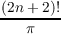 (P.V.)
(P.V.) 
