On an entire function of an entire function defined by Dirichlet series

K. N. Srivastava

Vol. 18 (1966), No. 2, 379–383

DOI: 10.2140/pjm.1966.18.379

Abstract

In this note we prove the following theorem which seems to exhibit an essential property of the order (R) of entire function defined by Dirichlet series.

Theorem If h(s) and g(s) are entire functions defined by Dirichlet series and g(log h(s)) is an entire function of finite order (R), then there are only two possible cases: either

(a) the internal function h(s) is a Dirichlet polynomial and the external function g(s) is of finite order (R); or

(b) the internal function h(s) is of finite order (R) and the external function g(s) is of order zero.

Here h(s) and g(s) are entire functions defined by the Dirichlet series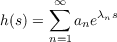

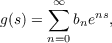satisfying the relations

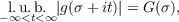for any real value of (in particular, every Dirichlet series absolutely convergent in the whole plane will have this property).

Mathematical Subject Classification

Primary: 30.56

Secondary: 30.24

Milestones

Received: 11 March 1965

Published: 1 August 1966