Über eine Beziehung zwischen Malcev-Algebren und Lietripelsystemen

Ottmar Loos

Vol. 18 (1966), No. 3, 553–562

DOI: 10.2140/pjm.1966.18.553

Abstract

A Malcev algebra is an anticommutative algebra which satisfies the identity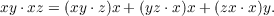

In this paper we construct to every Malcev algebra A a Lie triple system T_A and study the relations between them. A number of properties hold for a Malcev algebra if and only if they hold for the associated Lie triple system. E.g. the algebra A is solvable (semisimple, simple) if and only if T_A is. Moreover the radicals of A and T_A coincide. We shall prove:

Theorem A. A finite dimensional Malcev algebra A over a field of characteristics zero is semisimple if and only if the Killing form of A is nondegenerate.

Let C be the Cayley algebra over an algebraically closed field of characteristic zero. It has been shown by Sagle, that a simple 7-dimensional Malcev algebra A^∗ can be obtained from C. Using a further theorem of Sagle we prove

Theorem B. Every simple finite dimensional non-Lie Malcev algebra over an algebraically closed field of characteristic zero is isomorphic to A^∗.

Mathematical Subject Classification

Primary: 17.60

Secondary: 17.30

Milestones

Received: 1 May 1965

Published: 1 September 1966