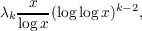|
Let φ(n) denote the Euler
function. The starting point of this paper is the simple observation that if p is a
prime then p and φ(p) + 1 = p have a common divisor which is greater than 1; its
conclusion is: if {mk} is the sequence of positive square free integers which have k
prime factors, where k ≧ 2, then the number of integers mk not exceeding x such
that mk and φ(mk) + 1 have a common divisor other than 1 is asymptotic
to
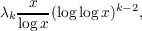
where λk is a positive constant that depends on k.
The source of the problem under consideration was a question raised by Gordon
in the course of his investigations of Hajós factorization of abelian groups. The
question was: are there integers n, other than primes and their doubles, such that
φ(n) + 1 divides n. This is still an open problem. However, if we relax our demands,
as we have done above, it is possible to prove the asymptotic relation stated
there.
|