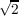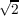|
A real quadratic form
Q = Q(x1,⋯,xn) is called copositive if Q(x1,⋯,xn) ≧ 0 whenever x1,⋯,xn ≧ 0. If we
associate each quadratic form Q = ∑
qijxixj qij = qji (i,j = 1,⋯,n) with a point
(q11,⋯,qnn,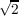 q12,⋯, q12,⋯,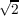 qn−1,n) of Euclidean n(n + 1)∕2 space then the copositive
forms constitute a closed covex cone in this space. We are concerned with
the extreme points of this cone. That is, with those copositive quadratic
forms Q for which Q = Q1 + Q2 (with Q1, Q2 copositive) implies Q1 = aQ,
Q2 = (1 − a)Q, 0 ≦ a ≦ 1. We show that if Q(x1,⋯,xn), n ≧ 2, is an extreme
copositive quadratic form then for any index i(1 ≦ i ≦ n), Q has a zero u with
u1⋯,un ≧ 0 where ui > 0. Further, using this fact, we establish an extension process
whereby extreme forms in n variables can be used to construct extreme form in n′
variables, for all n′ > n. qn−1,n) of Euclidean n(n + 1)∕2 space then the copositive
forms constitute a closed covex cone in this space. We are concerned with
the extreme points of this cone. That is, with those copositive quadratic
forms Q for which Q = Q1 + Q2 (with Q1, Q2 copositive) implies Q1 = aQ,
Q2 = (1 − a)Q, 0 ≦ a ≦ 1. We show that if Q(x1,⋯,xn), n ≧ 2, is an extreme
copositive quadratic form then for any index i(1 ≦ i ≦ n), Q has a zero u with
u1⋯,un ≧ 0 where ui > 0. Further, using this fact, we establish an extension process
whereby extreme forms in n variables can be used to construct extreme form in n′
variables, for all n′ > n.
|