Vol. 19, No. 2, 1966
Download this article
Download this article. For screen
For printing
Recent Issues
Vol. 332: 1  2
Vol. 331: 1  2
Vol. 330: 1  2
Vol. 329: 1  2
Vol. 328: 1  2
Vol. 327: 1  2
Vol. 326: 1  2
Vol. 325: 1  2
Online Archive
Volume:
Issue:
     
The Journal
About the journal
Ethics and policies
Peer-review process
 
Submission guidelines
Submission form
Editorial board
Officers
 
Subscriptions
 
ISSN 1945-5844 (electronic)
ISSN 0030-8730 (print)
 
Special Issues
Author index
To appear
 
Other MSP journals
Restricted bipartite partitions

L. Carlitz and David Paul Roselle
Vol. 19 (1966), No. 2, 221–228
DOI: 10.2140/pjm.1966.19.221
Abstract

Let πk(n,m) denote the number of partitions

n = n1 + n2 + ⋯ + nk
m = m1 + m2 + ⋯ + mk
subject to the conditions «««< Updated upstream
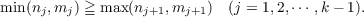min(nj,mj) ≧ max (nj+1,mj+1 ) (j = 1,2,⋅⋅⋅ ,k− 1).

Put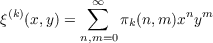

∑∞ ξ(k)(x,y) = πk(n,m )xnym n,m=0

We show that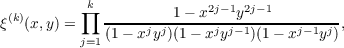

(k) ∏k ---------1−-x2j−-1y2j−1--------- ξ (x,y) = (1− xjyj)(1 − xjyj−1)(1− xj−1yj), j=1

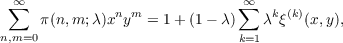
∑∞ n m ∑∞ k (k) π(n,m; λ)x y = 1+ (1− λ) λ ξ (x,y), n,m=0 k=1

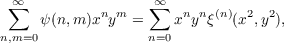∞∑ ∑∞ ψ(n,m)xnym = xnynξ(n)(x2,y2), n,m=0 n=0

where π(n,m;λ) denotes the number of “weighted” partitions of (n,m) and ψ(n,m) is the number of partitions into odd parts (nj, mj all odd).
Mathematical Subject Classification
Primary: 10.48
Milestones
Received: 20 March 1965
Published: 1 November 1966
Authors
L. Carlitz
David Paul Roselle